Armadura Vs Vida 2/2
En nuestro última entrada, que por si aun no la habéis leído os dejo aqui, dejamos todo planteado para saber que seria mejor, si comprar Armadura o Vida en el siguiente escenario:
- Vida = 0
- Armadura = 0
- Oro = 10.000
Sabiendo esto tenemos que definir nuestro objetivo, este será conseguir la máxima Vida Efectiva gastando 10.000 de Oro. Para ello tendremos que ver cual es el precio de un punto de Vida y de un punto de Armadura que unido a la ecuación de Vida Efectiva nos dará el ratio perfecto de Vida:Armadura y este nos indicara que debemos comprar en cada momento. Vamos al lió.
Eficiencia del Oro.
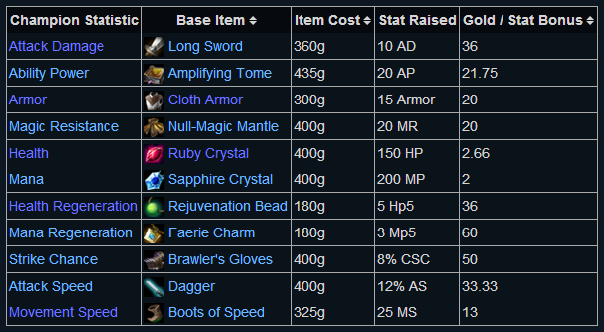
Os comentaba que lo primero sera saber cuanto vale un punto de Vida y cuanto uno de Armadura. Esto nos trae otro concepto muy utilizado para saber si un objeto es bueno por el precio que tiene o por el contrario es una basura. Para establecer este varemos se utilizan los objetos que solo aumentan una de nuestras stats y se divide el oro que cuesta entre el bonus de esa stats obteniendo el precio de un punto de esta stat. Os adjunto una tabla de leagueoflegends.wikia.com
Cálculo del Ratio
Fijándonos bien en lo que nos interesa vemos que cada punto de Armadura sale a 20 de Oro y cada uno de Vida a 2.66 de Oro. Ahora que ya sabemos cuanto vale cada uno y tenemos nuestro limite de 10.000 de Oro es cuestión de ver cuanto comprar de cada uno.
Marquemos ahora los limites, que serian comprar solo Vida y comprar solo Armadura:
- Solo Vida: En este caso tendríamos que por 10.000 de Oro podríamos comprar 3788 puntos de Vida.
- Solo Armadura: En el caso de gastarlo todo en armadura tendríamos 500 puntos de Armadura.
La Vida Eficiente que obtendremos en los dos casos sera:
- 0 Ar y 3788 V —–> 3788Ve
- 500 Ar y 0 V——–> 0 Ve
Conociendo los límites es fácil ver que el máximo de Vida Eficiente estará en un punto intermedio, y con esto no quiero decir justo a la mitad, de la tabla y aquí es donde esta la clave.
Recordemos que sabemos. Sabemos que el valor de Armadura estará entre 0 y 500 y el valor de Vida estará entre 0 y 3788 y que la suma de lo que nos gastemos en ambas tiene que sumar 10.000 de Oro. Esto expresado en una ecuación seria:
Donde:
Ar es la Armadura y V es la Vida.
Despejando la V tenemos que:
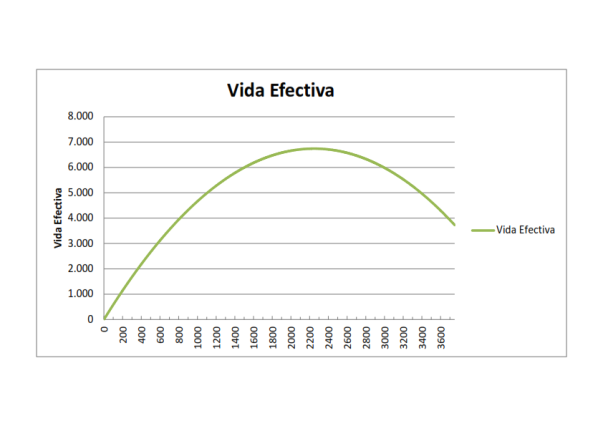
Dando valores a la Ar de 0 a 3788 obtendremos las valores de V. Es decir para Ar=100 tendremos que V=486 y por lo tanto aplicando lo visto en el anterior post, la Vida Eficiente para estos valores será de Ve=587. Si sustituimos la V en la formula de la Vida Eficiente para este escenario tendremos la siguiente gráfica donde se representa en el eje vertical la Ve y en el eje horizontal la V:
 Conclusiones
Conclusiones
Como podemos ver en la gráfica el valor máximo de Ve esta entre 2200 y 2300 de Vida, exactamente es de 2248 de Vida y le corresponde, según nuestra escenario, 200 puntos de Armadura. Sabiendo esto, está claro que el ratio mas optimo sera de 11 puntos de Vida por cada 1 de Armadura pero para recordarlo mejor y simplificar las cuentas:
10 puntos de Vida : 1 punto de Armadura
Es decir, por cada 10 puntos de vida deberemos tener 1 de Armadura. Con este simple calculo estaremos moviéndonos en este ratio y por lo tanto estaremos siempre en nuestra Vida Eficiente máxima y en consecuencia sacandole el máximo partido a nuestro Oro. Todo lo anteriormente explicado vale también para la Armadura Mágica tal y como explicamos en el post de ¿Como funciona la armadura?
Espero que os haya gustado y que ahora conozcáis un poco mas la mecánica del juego y en consecuencia podáis aprovecharla para mejorar vuestras partidas. Si hay algo que veáis que no cuadra o queráis una explicación más hacérnoslo llegar por los comentarios, o mejor aun decirnos sobre que queréis el próximo post relativo a mecánicas.
Relacionados:
Publicado el abril 16, 2014 en mecanica del juego y etiquetado en Armadura, Mecánica, Vida. Guarda el enlace permanente. 10 comentarios.
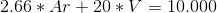
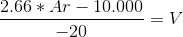
Buenísima la información y el esfuerzo en los cálculos 🙂
Una pregunta!
¿A qué fecha corresponderían estos calculos?
Buenísima la información y el esfuerzo en los cálculos 🙂
Una pregunta!
¿A qué fecha corresponderían estos calculos?
PD: sorry, no puse mi nombre xd
Pues si no ando desencaminado, están actualizados a dia de hoy. Nos alegra que te guste el articulo!
Amigo tengo una duda, cuando dices «Es decir para Ar=100 tendremos que V=486 y por lo tanto aplicando lo visto en el anterior post, la Vida Eficiente para estos valores será de Ve=587», pero la formula de ve es: ve=v*(ar*0,01), es decir con ar=100 y v=486 seria
ve=486*(100*0,01)= 486, ¿de donde sale el 587?? ahí me perdi xD.
Holas de nuevo:
otra consulta, si la armadura funciona igual q la magic resistance entonces podríamos concluir que
Cada 10 puntos de vida : es apropiado 1 punto de Magic Resistance?
Efectivamente chito, funciona exactamente igual!
«Si sustituimos la V en la formula de la Vida Eficiente para este escenario tendremos la siguiente gráfica donde se representa en el eje vertical la Ve y en el eje horizontal la V»
¿ESTARÍA MAL?
Porque si sustitumos V(Ar) en la fórmula de Ve(V,Ar) queda la funcion de Ve en función de Ar, (ya que no hay V, ha sido sustituida) Ve(Ar) y por lo tanto… ¿el eje horizontal sería Ar?
En conclusión, para un campeón asesino que en nivel 18 alcanza los 2.000 de vida máxima nos convendría armarle solo armadura/mr y como por ejemplo Zz’Rot + Angel guardián que nos llevaría a los 200 de armadura y mr en cuestión y ya con la vida estándar del champ en nivel 18 estaríamos óptimos. Lo demas es todo item’s de daño.
amigo te felicito, que gran labor. !!
Excelente explicación. Gracias genio! 🙂